【AdC2015】物理数学：反変ベクトルの共変微分

はじめに

　この記事はシリーズ「リーマン多様体上のラプラシアンを求めよう」の一つです。ラプラシアンの導出も合わせてお楽しみください。shitaro-happy-physics.hatenablog.jp

今日のお題

　歪んだ空間での微分、共変微分の式

を"導出"します*1。

　真っ直ぐな空間では平行移動は簡単です。ベクトルの各成分をそれぞれ同じ値に保ったまま移動すればいいのですから。一方、歪んだ空間では平行移動すると基底が変化してしまいます。この基底が変化することを成分の変化に押し付けたのが共変微分係数の式のクリストッフェル記号に表れているのです。

導出

　反変ベクトルの変換式の両辺を新しい座標\(x^{\mu'}\)で微分すれば目的の式が得られます。

　反変ベクトルの変換式

つまり

の両辺を新しい座標\(x^{\mu'}\)で微分すると

より

となります。

　次に、二階微分の項を消去します。Christoffel記号の変換式

※参考

より

つまり

を得ます。

　ところで、この式の形はテンソルの変換式そのものになっています。つまり

が2次の混合テンソルの成分であることを表します。この2次の混合テンソルの成分を共変微分係数と呼び、

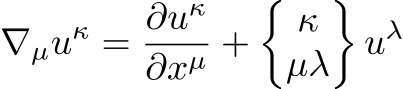
と書くのです。

一般的なテンソルの共変微分

　今回は1次反変テンソル(つまり反変ベクトル)についての共変微分係数を導出しました。ラプラシアンを導出するためにはこれで十分ですが、同様の計算を考えることでより一般的な議論をすることができます。
　一般的な混合テンソルの共変微分はなんと過去の自分がブログに残していました！ありがてぇ…

*1:共変微分係数の定義式なので、「導出」という言葉は不適切な気もする。