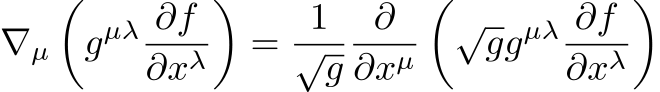今日のお題
今回から5日間は次の式の導出に関する話題を取り上げます。
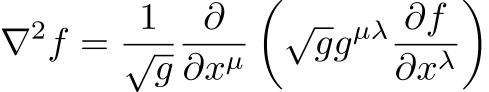
この式はリーマン多様体上のラプラシアン(Laplacian)、またはラプラス-ベルトラミ作用素(Laplace-Beltrami operator)と呼ばれています。
この公式さえ知っていれば、例えば3次元極座標(球座標)のラプラシアンをその場で導出することができます。
導出
勾配の発散を求めればLaplacianが得られます。
まず、スカラーの勾配(反変ベクトル)は次の式で与えられます。
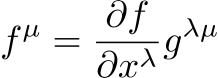
次に、反変ベクトルの発散を求めます。
反変ベクトルの共変微分
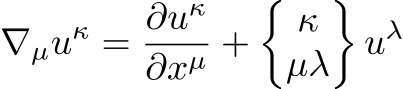
※参考
とクリストッフェル記号の関係式
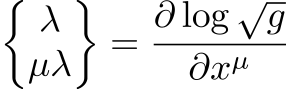
※参考
を使います。ここで、gは計量テンソル\(g^{\mu \nu}\)の行列式を表します。
反変ベクトルの共変微分の添字について縮約をする(つまり\(\mu=\kappa\)とする)と
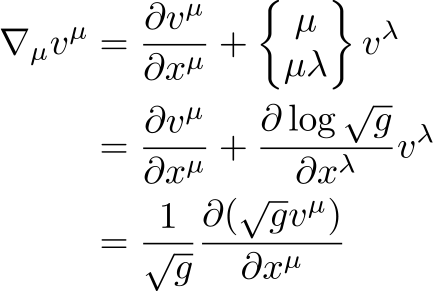
となります。これが反変ベクトルの発散です。
最後に、得られた反変ベクトルの発散にスカラーの勾配(反変ベクトル)を代入すると、目的の式が得られます。