【新歓展示に向けて】Merritt et al. 4-coil~イチヨウは作れる~No.2
シミュレーター篇
前回、尺の都合上シミュレーターに関しては結果のみを掲載しました。
【新歓展示に向けて】Merritt et al. 4-coil~イチヨウは作れる~No.1 - 幸福の物理
ここではシミュレーターについて解説をします。
この問題・・・rogyゼミでやった問題だ!
電流\( I\)、コイルの一辺の長さ\(L\)、原点-コイル間の距離\(d\)、求めたい磁場の座標\( (x,y,z)\)を入力することで磁場\(\boldsymbol{B}\)が得られる、というシミュレーターを作ることに決めました。
単純に入力に必要なパラメーターをコンストラクタの引数に取る場合、コンストラクタの引数が非常に冗長になってしまいます。また、一見するとコンストラクタの何番目の引数がどのパラメーターに対応しているのか分かりにくくなってしまいます。
こうしたときに役立つのがBuilderパターンであると先日行われた第二回rogyゼミで習いました!なので早速勉強して実装を試みました。
Builderパターン
Builderパターンとは、「作りたいオブジェクトの生成方法が複数なとき、ユーザーの代わりにそのオブジェクトを作る」という設計のこと(だと思います)。
Builder pattern - Wikipedia, the free encyclopedia
例えば、「家を建てる」ことを考えます:
- したろうは建築会社(Director)に家を建ててほしいと依頼します。
- 依頼された建築会社は家を建てるための手順を練ります。
- 建築会社は家の建築を大工(Builder)に依頼します。大工と一口にいっても和風建築専門や鉄筋コンクリート命など、さまざまな大工が存在します。
- 依頼された大工は建築会社が練った手順に従って建築をします。
Builderパターンは、次のような場合に効果的だそうです:
- 作り方は同じであるが、作られるものが違うとき。
- 作り方が複雑なために、ユーザーの代わりにオブジェクトを作りたいとき。
今回作りたいMerrittコイルシミュレーターでは、同じ作り方で作られるコイルが4つあるためにBuilderパターンが適用できそうですね。ここにMerrittコイルシミュレーターのクラス図を載せます:
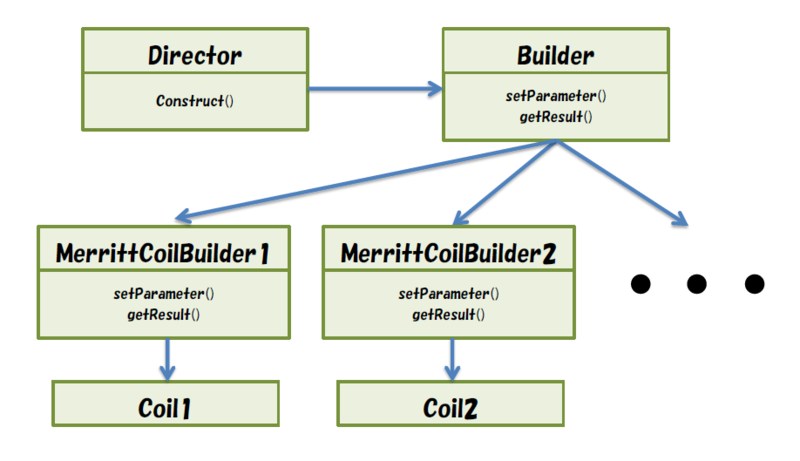
これを元に実装したのが次のプログラムです:
Computing the magnetic field which a Merritt 4-coi ...
このプログラムは「原点から30.25cm離れた場所に一辺が60cmの100回巻コイルを置き、それに5.2Aの電流を流したときにコイル中心に生じる\(z\)軸方向の磁場の大きさの数値解と解析解を表示する」ものです。ここで、解析解は
\begin{eqnarray}
B_{z}(0,0,z)
=
\frac{\mu_0I(2L)^2}{2\pi}
\frac{1}{\sqrt{z^2 + (L/2)^2/2}}
\frac{1}{z^2 + L^2}
\end{eqnarray}
で与えられます。詳しくは

- 作者: 砂川重信
- 出版社/メーカー: 岩波書店
- 発売日: 1987/01/29
- メディア: 単行本
- 購入: 1人 クリック: 7回
- この商品を含むブログ (4件) を見る
このプログラムによって、数値解と厳密解が等しいことが分かります。よって、このプログラムをもとにMerrittコイルシミュレーターを作っても信頼できるシミュレーションができると考えられます。
シミュレーション結果
さて、Builderパターンを用いたシミュレーション結果は次の図のようになりました:

↑前回の記事で見せたシミュレーション結果の画像です。Merrittコイルにより中心付近が平らになっているのが分かるでしょうか。
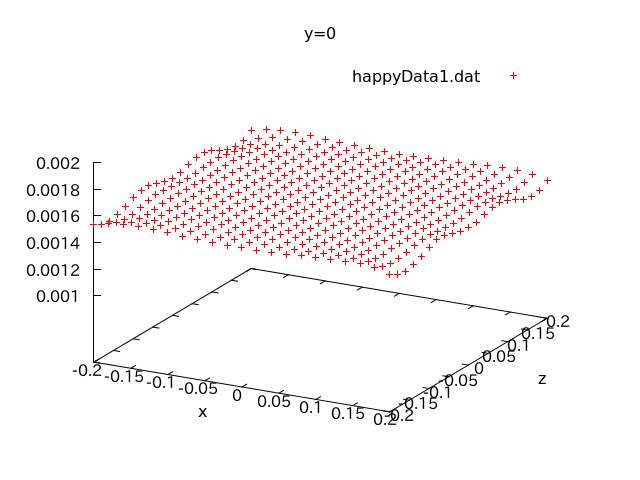
↑上図を拡大したもの。実験で使う領域、つまり40cm×40cmの空間における軸方向の磁場成分はほぼ一様であると言えるでしょう。
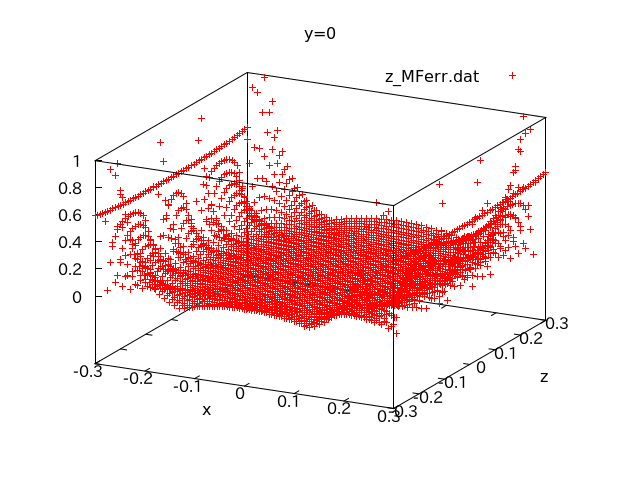
↑Merrittコイル内部全体の領域における軸方向の磁場の相対誤差です。実験で使う領域、つまり40cm×40cmの空間では中心磁場からの誤差が0.01%未満に収まっているから驚きです。幅広い空間に一様磁場が生じていることが分かります。
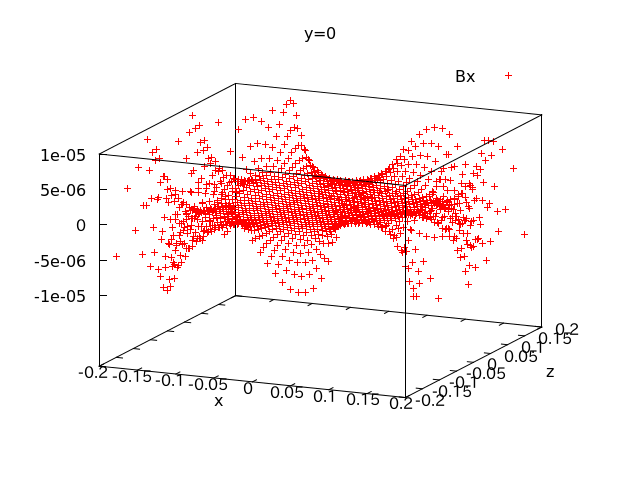
↑実験で使う領域、つまり40cm×40cmの空間における軸に垂直な成分の磁場をプロットしたもの。この磁場は軸方向の磁場に比べて最大\(10^{-2}\)オーダー小さいです。よって無視できる大きさであると言えます。
次は実物作成!
シミュレーションの結果、Merrittコイルによって自分の欲しい範囲に十分な一様磁場を生じさせることができることが分かりました。これで安心して実験装置を作ることができますね!
それではまた次回!